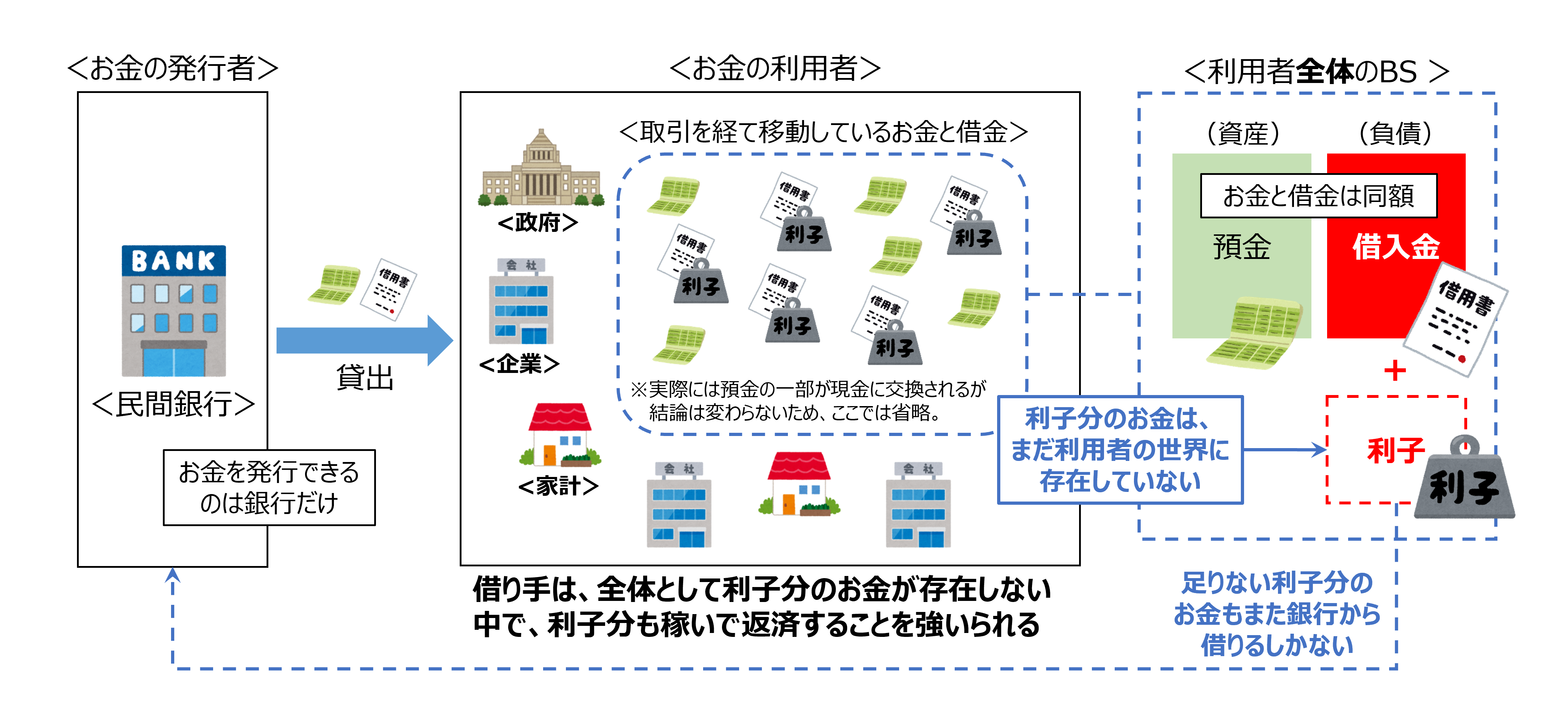

再び、お金の発行者と利用者という視点から利子を考えます。 お金を発行できるのは銀行だけであり、そのお金はすべて借金として利用者にもたらされます。 利用者の世界には、お金と同額の借金が常に存在しており、それらは様々な取引を通じて移動しています。 そして借金には利子が伴います。
仮に今、地球上のお金の総額(=借金の総額)が1京円であるとします。 また、全体の利子率の平均が1%であるとします。 この場合、全体の利子は100兆円(1京円×1%)となり、元金と利子を合わせた返済総額は1京100兆円となります。 では、利子分の新たな100兆円はどこにあるのでしょうか。 どこにもありません。 この時点で地球上には1京円のお金しか存在していないからです。
つまり、借金をした企業や個人は、全体のお金が元金分しか存在しない場所で、元金+利子分を返済するために競争しなければなりません。 その競争の形は商売であったり、時には戦争であったり様々です。 椅子取りゲームのように、限られたお金を奪い合う必要があります。 個別の企業や個人の話であれば、これ以上考えることはありません。 この世界は弱肉強食ですね、ということで話は終わります。
しかし、個別の企業や個人ではなく、地球上の借り手全体(=「お金の利用者」全体)を1つのグループと考えたとき、この借り手グループは、いま存在している以上のお金を返済しなければならないということになります。 なお、借り手グループの中には各国政府も含まれます。 上記の例では、1京円の枠の中で、1京100兆円の返済が必要です。
では、借り手グループは利子分の100兆円をどこから調達するのでしょうか。 銀行から借りるしかありません。 新たなお金は銀行でしか作られず、それが世の中に供給される方法は貸出のみだからです。 銀行からの貸出によって新たに100兆円が供給されれば、地球上のお金は当初の必要額を満たす1京100兆円になります。 しかし、今度はこの1京100兆円に対して1%の利子が発生します。
こうして、利子を支払うために新たな借金が必要となり、借金総額(=全体のお金)は複利でどんどん増えていきます。 地球上の借り手グループ全体が、まるで1人の多重債務者のような状況に陥っています。 このシステムの下では、全体として常に利子分のお金が足りないのです。
なお、常にお金が足りないと言っても、それはあくまで「お金の利用者」の世界に限った話です。 お金そのものは単なるデータに過ぎないため、「お金の発行者」はいくらでもお金を発行できます(参照:1-1. お金が生まれるとき)。 その意味で、現代の通貨システムでは「供給するお金が足りなくて困る」といった状況は発生しません。 しかし「お金の利用者」の世界では、どの時点でも元金分のお金だけが供給されていて、利子分のお金は存在していません。 このようにして、利用者全体としては常にお金が足りない、という状況が人為的に作られています。